The paper “Embedding-aided network dismantling”, co-authored by LASIGE’s integrated researcher Andreia Sofia Teixeira, was published in the journal Physical Review Research (SCIMAGO Q1). The work is a collaborative effort between LASIGE, Indiana University, Max Planck Institute for Dynamics and Self-Organization and the Cyprus University of Technology.

Optimal percolation concerns the identification of the minimum-cost strategy for the destruction of any extensive connected components in a network. Solutions of such a dismantling problem are important for the design of optimal strategies of disease containment based either on immunization or social distancing. Depending on the specific variant of the problem considered, network dismantling is performed via the removal of nodes or edges, and different cost functions are associated to the removal of these microscopic elements. In this paper, the researchers show that network representations in geometric space can be used to solve several variants of the network dismantling problem in a coherent fashion. Once a network is embedded, dismantling is implemented using intuitive geometric strategies. They demonstrate that the approach well suits both Euclidean and hyperbolic network embeddings. Their systematic analysis on synthetic and real networks demonstrates that the performance of embedding-aided techniques is comparable to, if not better than, the one of the best dismantling algorithms currently available on the market. The article is available here.

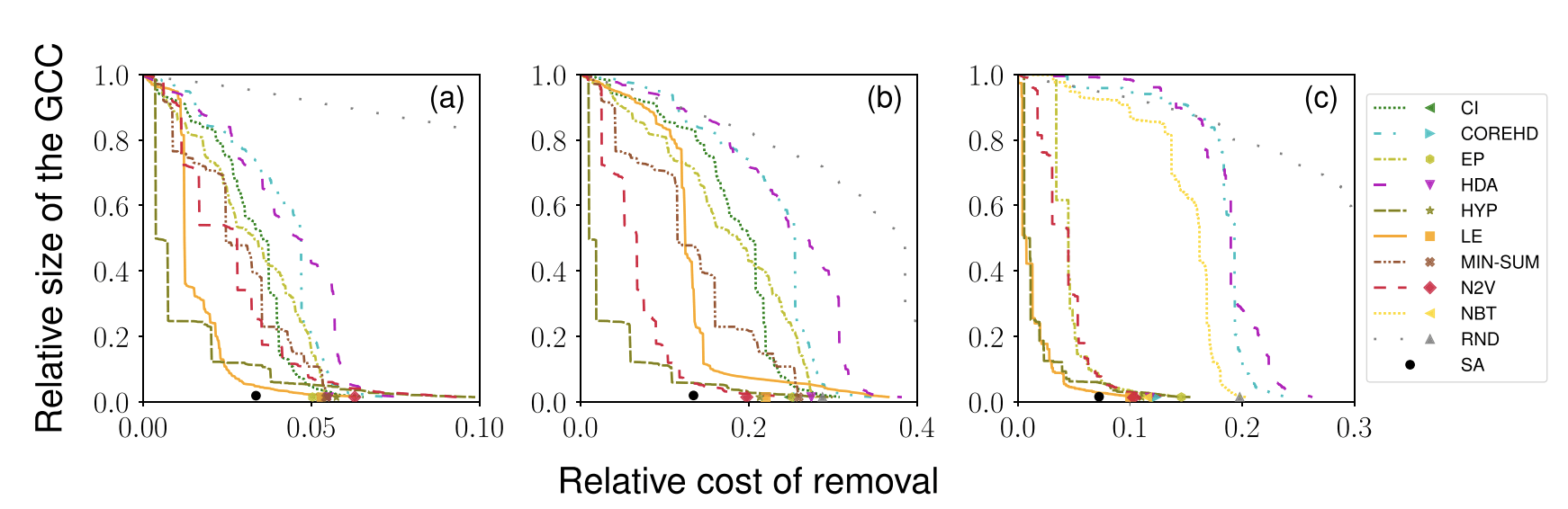
Image legend: Optimal percolation on the U.S. power grid. (a) Relative size of the giant connected component (GCC) as a function of the fraction of removed nodes. Different curves correspond to solutions obtained via the various dismantling methods (see Table I for the definition of the acronyms). Symbols present solutions to the problem of Eq. (2) obtained by the greedy postprocessing strategy started from the solution of a given algorithm. The network considered here is the U.S. power grid. (b) Same as in (a), but for the optimal site-percolation problem with degree cost. (c) Same as in (a), but for optimal bond percolation with unit cost.